🔥 오버라이딩 방지하기

때로는 메서드, 속성 또는 서브스크립트가 오버라이딩되는 것을 방지하고 싶을 수 있습니다. 이럴 때는 해당 요소를 final로 표시하면 됩니다. 메서드, 속성, 서브스크립트의 도입자 키워드(final var, final func, final class func, final subscript 등) 앞에 final 수정자를 작성하면 되죠.

서브클래스에서 final 메서드, 속성 또는 서브스크립트를 오버라이딩하려는 시도는 컴파일 타임 오류로 보고됩니다.

예를 들어, 다음과 같이 final 키워드를 사용하여 메서드를 오버라이딩할 수 없도록 할 수 있습니다:

class SuperClass {
    final func someMethod() {
        // 메서드 구현
    }
}
 
class SubClass: SuperClass {
    override func someMethod() {  // 컴파일 오류 발생!
        // 오버라이딩 시도
    }
}

class SuperClass {
    final func someMethod() {
        // 메서드 구현
    }
}
 
class SubClass: SuperClass {
    override func someMethod() {  // 컴파일 오류 발생!
        // 오버라이딩 시도
    }
}

SuperClass의 someMethod()는 final로 선언되었기 때문에, SubClass에서 이를 오버라이딩하려고 하면 컴파일 오류가 발생합니다.

익스텐션에 추가하는 메서드, 속성 또는 서브스크립트도 익스텐션 정의 내에서 final로 표시할 수 있습니다. 자세한 내용은 익스텐션을 참조하세요.

전체 클래스를 final로 표시하려면 클래스 정의의 class 키워드 앞에 final 수정자를 작성하면 됩니다(final class). final 클래스를 서브클래싱하려는 시도는 컴파일 타임 오류로 보고됩니다.

final class FinalClass {
    // 클래스 구현
}
 
class SubClass: FinalClass {  // 컴파일 오류 발생!
    // 서브클래싱 시도
}

final class FinalClass {
    // 클래스 구현
}
 
class SubClass: FinalClass {  // 컴파일 오류 발생!
    // 서브클래싱 시도
}

FinalClass는 final class로 선언되었기 때문에, 이를 서브클래싱하려고 하면 컴파일 오류가 발생합니다.

final 키워드는 상속 계층 구조를 설계할 때 매우 유용합니다. 상속되어서는 안 되는 클래스나 메서드, 속성 등에 final을 표시함으로써 의도치 않은 오버라이딩을 방지하고, 코드의 안정성과 예측 가능성을 높일 수 있죠.

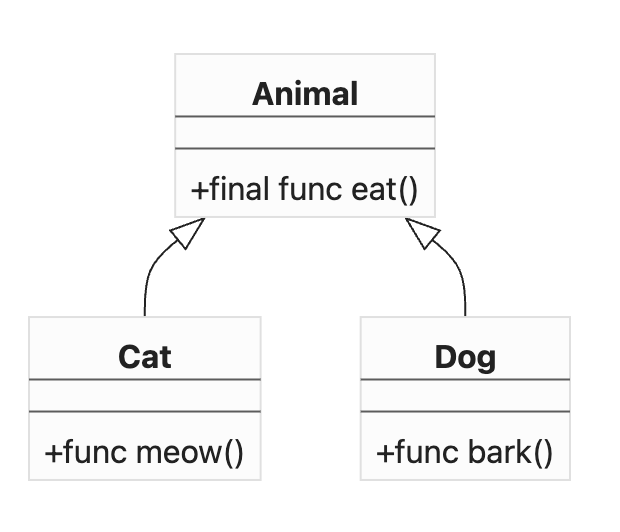
위의 다이어그램에서 Animal 클래스의 eat() 메서드는 final로 선언되어 있어, Cat이나 Dog 클래스에서 이를 오버라이딩할 수 없습니다. 반면에 meow()와 bark() 메서드는 각 서브클래스에서 자유롭게 구현할 수 있죠.

이렇게 final 키워드를 사용하여 오버라이딩을 선택적으로 제한함으로써 클래스 계층 구조를 더욱 견고하고 안전하게 만들 수 있습니다. 꼭 필요한 경우에만 상속과 오버라이딩을 허용하고, 그렇지 않은 경우에는 final로 막아두는 것이 좋은 설계 원칙이 될 수 있겠네요! 😄